We read every piece of feedback, and take your input very seriously.
To see all available qualifiers, see our documentation.
Have a question about this project? Sign up for a free GitHub account to open an issue and contact its maintainers and the community.
By clicking “Sign up for GitHub”, you agree to our terms of service and privacy statement. We’ll occasionally send you account related emails.
Already on GitHub? Sign in to your account
An ugly number is a positive integer whose prime factors are limited to 2, 3, and 5.
Given an integer n, return the nth ugly number.
Example 1:
Input: n = 10 Output: 12 Explanation: [1, 2, 3, 4, 5, 6, 8, 9, 10, 12] is the sequence of the first 10 ugly numbers.
Example 2:
Input: n = 1 Output: 1 Explanation: 1 has no prime factors, therefore all of its prime factors are limited to 2, 3, and 5.
Constraints:
解法一: 小顶堆+HashTable。如果x是丑数,则2x, 3x, 5x都是,放入小顶堆,拿出第n个即可。HashTable用于防止重复。代码如下:
class Solution { public: int nthUglyNumber(int n) { // 小顶堆 priority_queue<long, vector<long>, greater<long>> heap; unordered_set<long> hash; int cnt = 0; vector<int> mul{2, 3, 5}; heap.push(1); hash.insert(1); int tmp; for (int i = 0; i < n; i++) { tmp = heap.top(); heap.pop(); for (auto m: mul) { long next = (long)m * tmp; if (hash.count(next) == 0) { heap.push(next); hash.insert(next); } } } return tmp; } };
解法二: 动态规划,我直接cv,呵呵,真他妈快乐。 画了个图,模拟一下过程,其实就是一个多指针排序,哪是什么动态规划。
代码如下:
class Solution { public: int nthUglyNumber(int n) { int p2 = 1, p3 = 1, p5 = 1; vector<int> dp(n+1); dp[1] = 1; for (int i = 2; i <= n; i++) { int num2 = dp[p2] * 2, num3 = dp[p3] * 3, num5 = dp[p5] * 5; dp[i] = min(min(num2, num3), num5); if (dp[i] == num2) { p2++; } if (dp[i] == num3) { p3++; } if (dp[i] == num5) { p5++; } } return dp[n]; } };
The text was updated successfully, but these errors were encountered:
No branches or pull requests
An ugly number is a positive integer whose prime factors are limited to 2, 3, and 5.
Given an integer n, return the nth ugly number.
Example 1:
Example 2:
Constraints:
解法一:
小顶堆+HashTable。如果x是丑数,则2x, 3x, 5x都是,放入小顶堆,拿出第n个即可。HashTable用于防止重复。代码如下:
解法二:
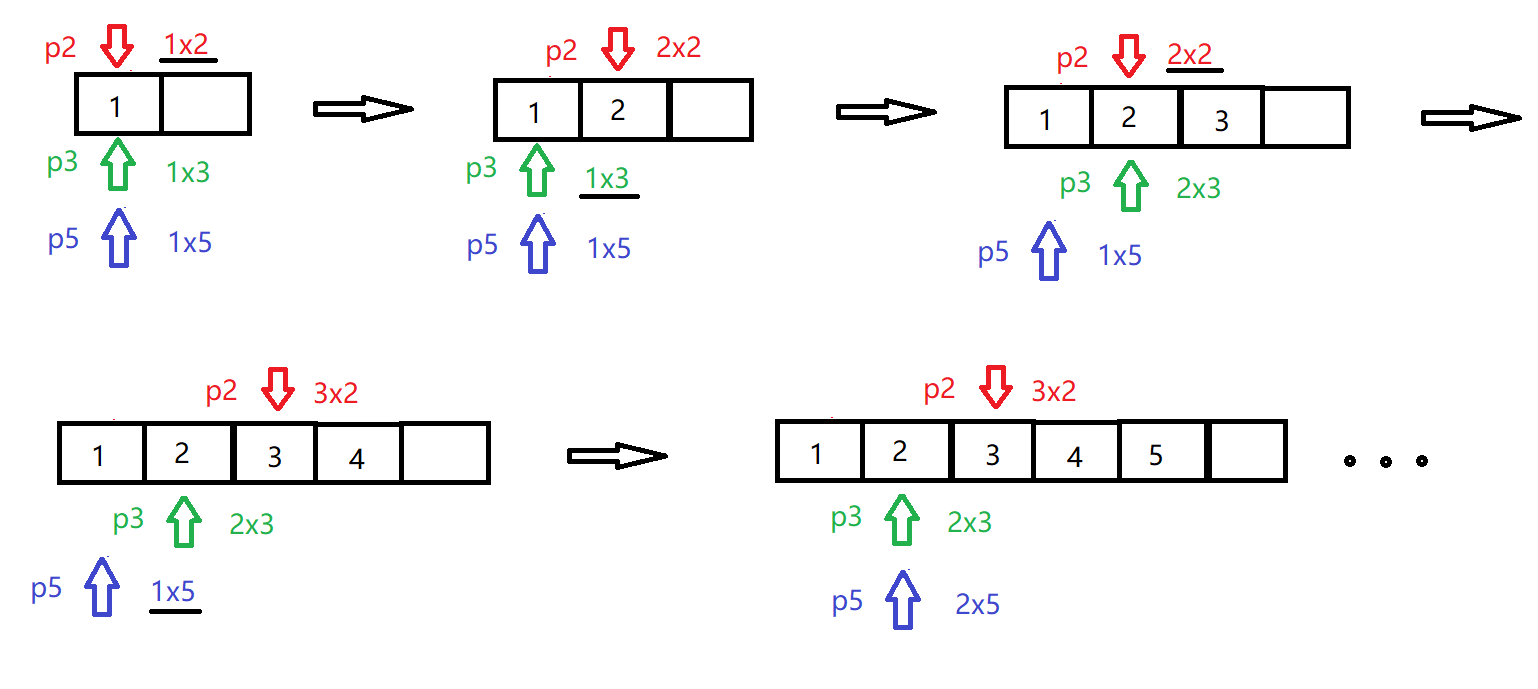
动态规划,我直接cv,呵呵,真他妈快乐。
画了个图,模拟一下过程,其实就是一个多指针排序,哪是什么动态规划。
代码如下:
The text was updated successfully, but these errors were encountered: