-
Notifications
You must be signed in to change notification settings - Fork 1
Open
Description
什么是图?
-
图是一种与树有些相似的数据结构。
- 实际上,在数学的概念上,树是图的一种。
- 我们知道树可以用来模拟很多现实的数据结构,比如:家谱/公司组织架构等等。
-
那么图长什么样子呢?或者什么样的数据使用图来模拟更合适呢?
- 人与人之间的关系网
- 互联网中的网络关系
- 广州地铁图
-
那么,什么是图呢?
- 我们会发现,上面的结点(其实图中叫顶点 Vertex)之间的关系,是不能使用树来表示(几叉树都不可以)。
- 这个时候,我们就可以使用图来模拟它们。
-
图通常有什么特点呢?
- 一组顶点:通常用 V (Vertex) 表示顶点的集合
- 一组边:通常用 E (Edge) 表示边的集合
- 边是顶点和顶点之间的连线
- 边可以是有向的,也可以是无向的。(比如 A --- B,通常表示无向。 A --> B,通常表示有向)
图的术语
术语
-
顶点
- 表示图中的一个结点。
- 比如地铁站中某个站/多个村庄中的某个村庄/互联网中的某台主机/人际关系中的人。
-
边
- 边表示顶点和顶点之间的连线。
- 比如地铁站中两个站点之间的直接连线, 就是一个边。
- 注意:这里的边不要叫做路径,路径有其他的概念,后面会区分。
-
相邻顶点
- 由一条边连接在一起的顶点称为相邻顶点。
- 比如
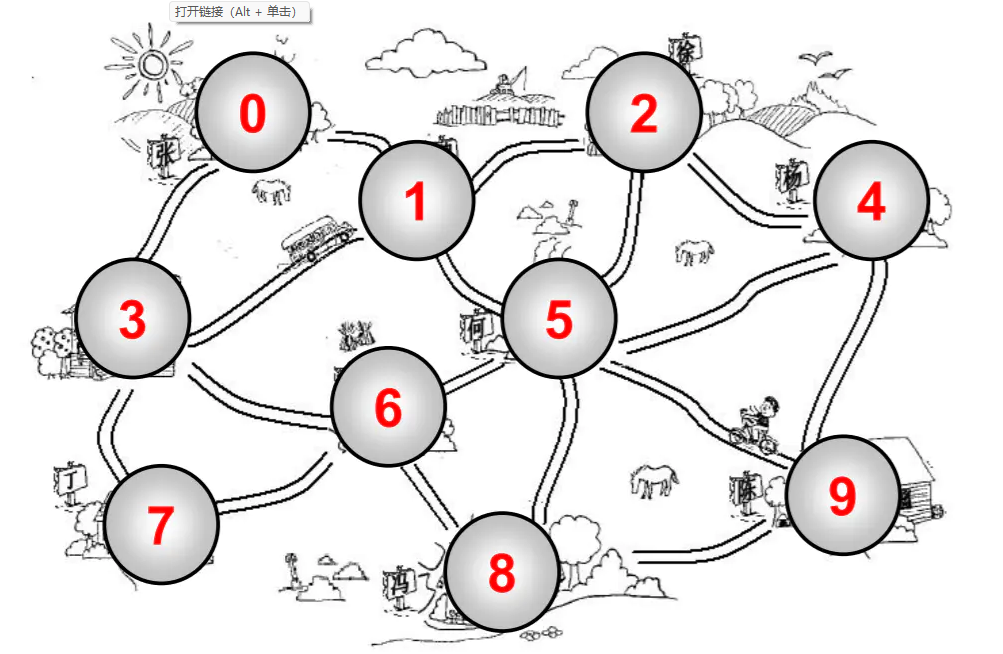
0 - 1是相邻的,0 - 3是相邻的。0 - 2是不相邻的。
-
度
- 一个顶点的度是相邻顶点的数量
- 比如 0 顶点和其他两个顶点相连,0 顶点的度是 2
- 比如 1 顶点和其他四个顶点相连,1 顶点的度是 4
-
路径
- 路径是顶点
v1,v2...,vn的一个连续序列, 比如上图中0 1 5 9就是一条路径。 - 简单路径: 简单路径要求不包含重复的顶点. 比如
0 1 5 9是一条简单路径。 - 回路:第一个顶点和最后一个顶点相同的路径称为回路。比如
0 1 5 6 3 0。
- 路径是顶点
-
无向图
- 上面的图就是一张无向图,因为所有的边都没有方向。
- 比如
0 - 1之间有边,那么说明这条边可以保证0 -> 1,也可以保证1 -> 0。
-
有向图
- 有向图表示的图中的边是有方向的。
- 比如
0 -> 1,不能保证一定可以1 -> 0,要根据方向来定。
无权图和带权图
-
无权图
- 我们上面的图就是一张无权图(边没有携带权重)
- 我们上面的图中的边是没有任何意义的,不能说
0 - 1的边,比4 - 9的边更远或者用的时间更长。
-
带权图
- 带权图表示边有一定的权重
- 这里的权重可以是任意你希望表示的数据:比如距离或者花费的时间或者票价。
- 一张有向和带权的图
现实建模
- 对交通流量建模
- 对飞机航线建模
图的封装
创建图类
- 先来创建 Graph 类,定义了两个属性:
vertexes用于存储所有的顶点,使用一个数组来保存。adjListadj 是 adjoin 的缩写,邻接的意思。adjList 用于存储所有的边,这里采用邻接表的形式。
class Graph {
constructor() {
this.vertexes = []; // 存储顶点
this.adjList = new Dictionay(); //存储边信息
}
}添加方法
- 添加顶点:可以向图中添加一些顶点。
- 将添加的顶点放入到数组中。
- 另外,给该顶点创建一个数组
[],该数组用于存储顶点连接的所有的边.(回顾邻接表的实现方式)
// 添加顶点
addVertex(val) {
// 添加点
this.vertexes.push(val)
// 添加点的关系 采用邻接矩阵法 结构用Map
this.adjList.set(val, [])
}- 添加边:可以指定顶点和顶点之间的边。
- 添加边需要传入两个顶点,因为边是两个顶点之间的边,边不可能单独存在。
- 根据顶点 v 取出对应的数组,将 w 加入到它的数组中。
- 根据顶点 w 取出对应的数组,将 v 加入到它的数组中。
- 因为这里实现的是无向图,所以边是可以双向的。
// 添加边
addEdge(val1, val2) {
// 添加边需要传入两个顶点, 因为边是两个顶点之间的边, 边不可能单独存在.
// 这里实现的是无向图, 所以这里不考虑方向问题
this.adjList.get(val1).push(val2)
this.adjList.get(val2).push(val1)
}Metadata
Metadata
Assignees
Labels
No labels